DOI: https://doi.org/10.18601/17941113.n12.04
Propuesta metodológica para la valoración de opciones sobre tasa de cambio USD-COP
Carlos Castañeda Acosta*
* Magíster en Finanzas. Trader. Gerencia Financiera. Seguros Bolívar, Bogotá (Colombia). [carlos.castaneda@segurosbolivar.com].
Fecha de recepción: 27 de junio de 2017. Fecha de aceptación: 15 de julio de 2017.
Para citar este artículo: Castañeda Acosta, C. (2017). Propuesta metodológica para la valoración de opciones sobre tasa de cambio USD-COP. ODEON, 12, pp. 77-117.
Resumen
Se presenta una propuesta metodológica para resolver el problema de la valoración de opciones sobre tipo de cambio en el mercado colombiano. Se realiza una breve revisión de las características del mercado de tasa de cambio local, se discuten algunas metodologías de valoración, y se procede a aplicar estas metodologías como propuesta para la valoración de opciones europeas sobre tipo de cambio, describiendo algunos resultados que resultan deseables en el marco de las condiciones de mercado.
Palabras clave: valoración de opciones, tipo de cambio, procesos estocásticos. Clasificación jel: G13, C02, C67
Abstract
We present a methodological proposal to solve the problem of the options pricing over exchange rate in the Colombian market. We perform a brief review of the characteristics of local exchange market, discuss some valuation methodologies, and proceed to apply these methodologies as a proposal for the valuation of European options on exchange rate, describing some results that are disables in the framework of market conditions.
Key words: Options pricing, exchange rate, stochastic processes. jel Codes: G13, C02, C67
Introducción
Desde su publicación en 1973, el modelo de valoración de opciones desarrollado por Fisher Black y Myron Scholes se ha convertido en un estándar para el sector financiero a nivel global, y su uso, tanto por las mesas de negociación como por la academia, lo ha convertido en uno de los pilares de las finanzas modernas. Como todo modelo, parte de unos supuestos que permiten su aplicación, y son precisamente estos supuestos la base de numerosas discusiones sobre la certeza de sus resultados.
En los últimos años se han presentado significativos avances que han permitido, mediante el abandono de uno o varios de estos supuestos, desarrollar metodologías de valoración consistentes con el principio de no arbitraje y que reflejan adecuadamente el comportamiento de los activos que sirven como subyacentes, o condiciones del mercado particulares que no son capturadas por el modelo Black-Scholes original, como la estructura de volatilidad o la de tasas de interés.
En este documento se realiza una introducción a la valoración de opciones en el mercado colombiano, en particular, sobre tipo de cambio dólar-peso. Primero, se realiza una breve revisión de las características del mercado de tasa de cambio local, luego se presentan algunas metodologías de valoración, y, finalmente, se muestra la aplicación de estas metodologías como propuesta para la valoración de opciones europeas sobre tipo de cambio, describiendo algunos resultados que son deseables en el marco de las condiciones del mercado local colombiano. Como desarrollo adicional se presentan los algoritmos creados a lo largo de la investigación, con el fin de que sirvan como insumo en futuros estudios.
1. Características del mercado cambiario en Colombia
1.1 Tipo de cambio y mercado cambiario
La tasa de cambio es la cantidad de una moneda que se paga por otra. Según la Resolución Externa No. 8 de 2000 del Banco de la República, el mercado cambiario está constituido por la totalidad de las divisas que deben canalizarse obligatoriamente por conducto de los intermediarios autorizados para el efecto o a través del mecanismo de compensación previsto.
1.2 Operaciones autorizadas en el mercado cambiario
Las operaciones que deben canalizarse obligatoriamente a través del mercado cambiario son las siguientes:
1.3 Intermediarios autorizados
Son intermediarios del mercado cambiario (IMC):
1.4 Algunos tipos de regímenes de tasa de cambio
1.4.1 Régimen de tasa de cambio fija
Bajo este esquema, el Banco Central se compromete a que la tasa de cambio se mantendrá en un valor predeterminado. En el escenario en que el mercado presente un exceso en la demanda de divisas, el Banco Central suministra al mercado las divisas necesarias para mantener la tasa de cambio en su valor prefijado. De la misma forma, cuando se presentan excesos de oferta, el Banco Central compra las divisas para evitar la caída de la tasa de cambio.
1.5 Régimen de banda cambiaria
En 1994, Colombia adoptó un régimen de banda cambiaria, el cual representa un esquema intermedio entre un régimen de tasa de cambio fija y otro de flotación libre. La banda cambiaria está definida por los límites dentro de los cuales puede fluctuar la tasa de cambio.
1.5.1 Estructura de la banda cambiaria
Tasa máxima: también conocida como tasa techo, corresponde al nivel máximo de la tasa que el Banco Central está dispuesto a permitir en el mercado interbancario de dólares. Cuando las fuerzas de oferta y demanda del mercado llevan la tasa de cambio a este nivel, el Banco Central interviene para vender tantos dólares como sea necesario para mantener la tasa de cambio en este valor. La tasa máxima o techo varía diariamente, dependiendo de la pendiente de la banda cambiaria.
Tasa mínima: también conocida como tasa piso, corresponde al nivel mínimo de la tasa que el Banco Central está dispuesto a permitir en el mercado interbancario de dólares. Cuando el mercado lleva la tasa a este nivel, el Banco Central interviene para comprar tantos dólares como sea necesario para que el tipo de cambio se mantenga en este valor. Al igual que la tasa máxima, depende de la pendiente de la banda cambiaria.
Pendiente de la banda cambiaria: corresponde al porcentaje anual de devaluación que se aplica a la tasa piso y a la tasa techo.
Amplitud de la banda cambiaria: es la distancia que existe entre la tasa piso y la tasa techo. Está definida como un porcentaje medido desde un punto medio.
1.6 Régimen de tasa de cambio flexible
En este régimen el Banco Central se abstiene de intervenir, por lo que la tasa de cambio está totalmente determinada por la oferta y la demanda de divisas en el mercado. A partir del 25 de septiembre de 1999, fue eliminado en Colombia el sistema de banda cambiaria y se adoptó un sistema de libre flotación del tipo de cambio nominal.
Respecto al desmonte de la banda cambiaria, en septiembre de 1999, varios autores, entre ellos miembros de la junta directiva del Banco de la República en el momento, han señalado las razones por las cuales se optó por este giro en la política. Según Villar (1999), era necesario un proceso de ajuste cambiario desde finales de la década de los noventa, luego de la fuerte revaluación del peso que se había presentado en los años anteriores, y, por otra parte, el mantenimiento del régimen de bandas cambiarias requiere no solo el compromiso del Banco Central, sino del apoyo decidido del Gobierno y de la comunidad financiera internacional; según Villar, para la época era evidente que dicho apoyo había dejado de existir. En este contexto, el autor concluye que el esquema de bandas cambiarias era insostenible.
Por otra parte, respecto a los resultados del cambio en política, otros autores (Clavijo, 2001) concluyen que gracias a la creciente flexibilidad cambiaria de finales de los años noventa, y el ajuste fiscal adelantado simultáneamente, Colombia logró reducir su inflación a tasas inferiores a un dígito, manteniendo una tasa de cambio real más competitiva. El déficit del sector público no financiero se redujo de niveles cercanos al 5 % a cerca de 2,6 % del PIB durante 1999-2001, mientras que la inflación se mantuvo por debajo del 10 % anual.
1.7 Mecanismos de intervención del Banco de la República en el mercado cambiario
El Banco de la República cuenta con dos alternativas para intervenir el mercado cambiario, a saber:
- Intervención mediante subasta de opciones. El Banco de la República puede intervenir a través de subastas de opciones americanas put (las cuales dan al tenedor el derecho de vender dólares al Banco de la República) o call (que otorgan el derecho a comprar dólares al Banco de la República). Este mecanismo fue adoptado en noviembre de 1999, bajo el régimen de libre flotación de la tasa de cambio.
La subasta de opciones puede tener dos propósitos:
- Acumular o desacumular reservas internacionales.
- Controlar la volatilidad de la tasa de cambio.
- Acumulación o desacumulación de reservas internacionales
Acumulación de reservas internacionales: el Banco de la República puede convocar y realizar mensualmente, una subasta de opciones put por un monto discrecional. La convocatoria de la subasta se debe realizar como mínimo con un día hábil de anticipación. Las opciones put se pueden ejercer en el plazo comprendido entre el primer y el último día hábil del mes siguiente al cual se realiza la subasta (generalmente mes calendario), o en el plazo que determine la convocatoria. Las opciones pueden ejercerse durante su plazo de manera parcial o total, cualquier día hábil siempre que esté habilitada la condición de ejercicio. La condición de ejercicio se activa cuando la TRM (tasa representativa del mercado certificada por la Superintendencia Financiera de Colombia) sea inferior a su promedio móvil de los últimos veinte días hábiles.
Desacumulación de reservas internacionales: de manera ocasional, el Banco de la República puede anunciar una subasta de opciones call. Se cumplen las mismas condiciones de convocatoria, plazos y liquidación en ejercicio (parcial o total) de las opciones put; sin embargo, la condición de ejercicio es que la TRM sea superior a su promedio móvil de los últimos 20 días hábiles.
1.8 Control de volatilidad de la tasa de cambio
La convocatoria de estas subastas requiere que la TRM se encuentre en un nivel menor o igual a 7 % (venta de opciones put ) o en un nivel mayor o igual a 7 % (venta de opciones call ) de su promedio móvil de los últimos 20 días hábiles y se haya vencido el plazo de las opciones put o call de la última subasta para el control de la volatilidad, sea que estas hayan sido ejercidas o no. El cupo de estas subastas se ha establecido en US$ 500 millones actualmente, y el plazo corresponde a 1 mes contado desde el día de la subasta. Las opciones se pueden ejercer cualquier día hábil durante su plazo (americanas), siempre y cuando la TRM se encuentre en un nivel menor o igual a 7 % para el caso de las opciones put o en un nivel superior o igual a 7 % para el caso de las opciones call.
1.8.1 Intervención directa
El Banco de la República puede realizar operaciones de intervención directa con los intermediarios del mercado cambiario (IMC) o intermediarios de las opciones cambiarias (OIC), y con las sociedades comisionistas de Bolsa que hayan demostrado que cumplen con los requisitos para ser considerados IMC. En este tipo de intervención, el Banco de la República realiza operaciones de compra y venta de dólares directamente en el mercado spot (o en el mercado de opciones de los OIC) con los mismos propósitos descritos anteriormente. Si el Banco desea acumular reservas internacionales o disminuir la volatilidad a la baja de la tasa de cambio, puede comprar dólares directamente; en caso contrario, si desea desacumular (temporal u ocasionalmente) reservas o disminuir la volatilidad al alza de la tasa de cambio, puede vender dólares en el mercado spot.
2. Algunos modelos para la valoración de opciones sobre divisas
2.1 Modelo de Garman-Kohlhagen
El modelo clásico de valoración de opciones Black-Scholes no se adapta correctamente a las opciones sobre tipo de cambio, ya que en estas últimas se involucran varias tasas de interés de formas que difieren de los supuestos básicos de Black-Scholes (Garman y Kohlhagen, 1983). Con el fin de resolver este problema, Garman-Kohlhagen desarrollan una propuesta de valoración de opciones sobre divisas, la cual relacionan a los trabajos obtenidos por Black (1976) en su modelo de valoración de opciones sobre commodities, y Samuelson-Merton (Merton, 1976) en su modelo de dividendos proporcionales.
Garman-Kohlhagen explican que la diferencia entre una opción sobre tipo de cambio y una opción sobre una acción que no paga dividendos (activo bajo el cual se desarrolla el modelo Black-Scholes) son los precios forward de equilibrio. Bajo esta premisa, al mantener las tasas de interés constantes (supuesto básico de Black-Scholes), el precio forward de la acción debe incluir una prima igual a la tasa de interés (Garman y Kohlhagen, 1983); sin embargo, en el mercado cambiario, los precios forward pueden incluir primas positivas o negativas (caso referido por los autores como descuento). Lo anterior obedece a que el valor forward de una divisa está relacionado la ratio del precio de los bonos libres de riesgo que se negocian en cada país. Según la ley de paridad de tasas de interés, la cual es una condición de no arbitraje, la prima de un forward de divisas debe ser igual al diferencial de tasas de interés, que puede ser positivo o negativo (Garman y Kohlhagen, 1983). Ya que tanto las tasas de interés domésticas como las tasas de interés del exterior afectan la valoración de los contratos forward, es lógico esperar que esta relación se mantenga en la valoración de opciones.
2.1.1 Supuestos del modelo
2.1.2 Dinámica del subyacente
De acuerdo con lo anterior, la dinámica del subyacente se representa de la forma (diferencial):
Donde:
S: precio spot de la divisa entregable (unidades de divisa doméstica por 1 unidad de divisa del exterior).
μ: componente de tendencia del precio spot de la divisa.
σ: componente de volatilidad del precio spot de la divisa.
Ζ: proceso de Wiener.
Trabajando en una economía similar a la de Black-Scholes (1973), los supuestos implican que no existen oportunidades de arbitraje y se presenta un esquema de tiempo continuo, por lo que el exceso de retorno esperado ajustado por riesgo de todos los activos debe seguir la forma:
donde:
a i : retorno esperado de cualquier activo "i" de la economía.
rD: tasa de interés doméstica libre de riesgo.
δi: desviación estándar de los retornos del activo "i".
λ : exceso de retorno.
Se puede observar que λ no depende de ninguno de los activos de la economía. Al aplicar sobre la tenencia de la divisa del exterior se obtiene:
donde rF es la tasa de interés del exterior libre de riesgo.
Esto implica que el retorno esperado de mantener la divisa del exterior es μ, la tendencia de la tasa de cambio expresada en unidades de divisa doméstica por 1 unidad de divisa del exterior, más el retorno libre de riesgo derivado de mantener la divisa del exterior en la forma de un activo seguro, como un bono soberano, el cual paga intereses de rF; σ representa la desviación estándar de los retornos de la divisa del exterior. Los autores destacan que los parámetros μ, rD, rF y σ no tienen dimensión (están expresados como escalar en porcentaje), por lo que no se presenta el problema de conversión en términos de unidades domésticas o del exterior, ya que se da un ajuste que se explicará más adelante (Garman y Kohlhagen, 1983).
Ahora, se define C(S,T) como el precio de una opción call europea con Tcomo el tiempo que resta para el vencimiento, aplicando (2) se obtiene:
donde ac y δc son la tasa de retorno esperada del call y la desviación estándar de los retornos respectivamente. Aplicando el lema de Ito se llega a:
Al sustituir (5) y (6) en (4) se obtiene:
Igualando (4) y (7),
La ecuación (8) guarda una estrecha relación con los resultados obtenidos por Samuelson (1965) y Samuelson y Merton (1969), en estos modelos la tasa de retorno esperada de los dividendos (dividend yield) se asume proporcional al nivel actual del precio de la acción. Garman-Kohlhagen afirman que la interpretación para las opciones sobre divisas es similar, ya que rF puede ser considerada la tasa de los dividendos de la divisa del exterior; sin embargo, ya que esta tasa se encuentra expresada en términos de la tasa de cambio del exterior, debe ser convertida a términos de la divisa local, multiplicando por la tasa de cambio spot S (Garman y Kohlhagen, 1983). Bajo el modelo de Samuelson-Merton, una compañía debe monitorear constantemente el nivel de precio spot de su acción y ajustar los dividendos para mantener la proporción constante, supuesto que es poco práctico en el mundo real. Por el contrario, en el mercado cambiario el ajuste de conversión de divisa del exterior a doméstica se da automáticamente, como se observa en (8).
2.1.3 Fórmula de valoración
La solución de (8) para el precio de una opción call europea debe obedecer la siguiente condición de frontera:
donde:
K: precio strike o de ejercicio de la opción.
Lo anterior lleva finalmente a la expresión de la opción call europea sobre divisas (Garman y Kohlhagen, 1983):
donde:
con
N(χ) = función de distribución acumulada normal estándar.
La ecuación (8) es la expresión para hallar el valor de cualquier activo que cumpla con los supuestos explicados, por lo que Garman-Kohlhagen (1983) afirman que el precio de una opción put europea también satisface la ecuación diferencial, pero con una condición de frontera diferente, a saber:
Por lo que la solución de (8) lleva a la expresión de la opción put europea sobre divisas:
donde la expresión para x es la misma del call.
2.2 Modelo de difusión con saltos de Merton
Uno de los supuestos críticos en el modelo de Black-Scholes es que la dinámica de los retornos del activo subyacente puede ser descrita por un proceso estocástico de difusión continua (GBM). Merton (1976) afirma que la validez de la fórmula Black-Scholes depende de si los cambios en el precio del subyacente son pequeños en un intervalo de tiempo pequeño. Por esto, Merton desarrolla un modelo para el caso de que los retornos sean generados por la combinación de procesos continuos y procesos con saltos.
2.2.1 Supuestos del modelo
2.2.2 Dinámica del subyacente
De acuerdo con Merton, el cambio total en el precio del subyacente es la combinación de dos tipos de cambios: el "ruido" normal en el precio (componente modelado a través del GBM estándar con varianza constante por unidad de tiempo), y los movimientos repentinos o "anormales" que son resultado de la aparición de nueva información relevante (componente modelado a través de un proceso Poisson dada su naturaleza de presentarse en momentos discretos en el tiempo) (Merton, 1976).
El salto, descrito como un evento con distribución Poisson, es la aparición de nueva información relevante sobre el subyacente. Se asume que dichas apariciones (saltos) son i.i.d (independientes e idénticamente distribuidas); dado esto, la probabilidad de que ocurra un evento (salto) durante un intervalo de tiempo h puede ser descrito como:
donde:
0(h ): asíntota definida por ψ(h) = 0(h) si lím
λ parámetro de la distribución Poisson, número de saltos por unidad de tiempo. La ecuación diferencial estocástica que describe el comportamiento de los retornos del subyacente bajo estas condiciones se expresa de la siguiente forma:
donde:
S: precio spot del subyacente.
a: retorno esperado del subyacente.
k = ε(γ-l) = ε(γ)-1
(Y- 1): variable aleatoria de cambio en porcentaje en el precio del activo si ocurre el evento Poisson (si se presenta un salto).
ε: valor esperado.
σ2: varianza de los retornos del precio del activo, condicional a la ausencia del evento Poisson.
dΖ: proceso Wiener estándar.
q(t): proceso Poisson independiente.
La ecuación diferencial que describe la dinámica del subyacente permite observar que σdZ describe a lo que Merton (1976) se refiere como ruido normal, mientras dq describe los movimientos anormales (saltos). Si se trabajara bajo el supuesto de λ = 0 (lo que implica dq = 0), la ecuación diferencial de la dinámica del subyacente sería la misma de Black-Scholes, por lo que (15) podría expresarse como:
donde, con probabilidad 1, no ocurre más de un evento Poisson en un instante, y si ocurre el evento de salto (Y-1) es una función que produce el salto finito desde S a SY. El camino resultante de este proceso para S(t) será continuo con saltos finitos de diferentes signos y amplitudes que ocurren en momentos discretos del tiempo. Si a, λ, k σ se mantienen constantes, la relación entre S(0) y S(t) puede describirse como:
donde:
Z(t): variable aleatoria de distribución normal con μ = 0 y σ2= t
Y(n): 1 para n = 0.
γ(n) :
para n ≥ 0.
Yj : secuencia de variables aleatorias independientes e idénticamente distribuidas que expresan el cambio en el precio si ocurre un salto.
n: número de saltos, variable con distribución Poisson con parámetro λt.
Ahora, se define W como el precio de una opción call europea, y suponiendo que el precio de la opción sigue una dinámica similar a la del subyacente descrito anteriormente (acción), la dinámica del activo contingente puede describirse como:
donde:
aw : tasa de retorno esperada de la opción.
σ2W: varianza del retorno esperado de la opción, condicional a la ausencia del salto.
qW (t): proceso Poisson independiente con parámetro λ.
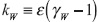
(γ w - 1) : variable aleatoria de cambio en porcentaje en el precio de la opción si ocurre el evento Poisson (si se presenta un salto).
ε: valor esperado.
Aplicando el lema de Ito se obtiene:
donde:
F(S,t) indican derivadas parciales del precio de la opción call.
Siguiendo el análisis de Black-Scholes, y continuando con la metodología empleada en el modelo de Garman-Kohlhagen para garantizar la ausencia del arbitraje, el retorno de la opción call debe ser igual a la tasa libre de riesgo; si se trabaja bajo el supuesto de λ = 0 (por consiguiente dq = dq = 0), se llega a:
2.2.3 Fórmula de valoración
A partir de (20), (21) y (22), bajo las condiciones mencionadas para λ y dq, se puede llegar a la ecuación diferencial de Black-Scholes. Sin embargo, Merton resalta que en presencia del proceso de saltos dq, no es posible encontrar un set de portafolio réplica (compuesto por el subyacente y una opción) que retorne la tasa libre de riesgo, ya que la combinación de activos del portafolio es una operación lineal, mientras el precio de la opción es una función no lineal del precio del subyacente (Merton, 1976). Por esto, Merton señala como alternativa la propuesta de Samuelson (1965), en la que si se expresara el retorno esperado de la opción como función del precio spot del subyacente y el tiempo al vencimiento, se podría derivar una fórmula para el precio del activo contingente.
Entonces, se define g(S, t) como la tasa instantánea de retorno de equilibrio de la opción cuando el precio spot del subyacente es S y la opción expira en el momentoAQUI VA SIMBOLOen el futuro. Bajo estas condiciones, la ecuación diferencial estocástica para la opción call europea puede expresarse de la siguiente forma:
Sujeta a las siguientes condiciones de frontera:
donde:
E: strike o precio de ejercicio de la opción
Sin embargo, (23) aún expresa el precio del call bajo a y g(S, t), por lo que tomando (22), (20) y (21), (23) puede expresarse:
Puede llegarse a (25) ya que gracias a (22), el retorno esperado de un portafolio de cobertura con beta=0 debe ser igual a la tasa libre de riesgo r; en otras palabras, (22) implica el retorno esperado de un portafolio compuesto por un activo riesgoso y la opción ap = r. La ecuación (25) puede reducirse a la ecuación de Black-Scholes si λ = 0.
Una vez especificada la ecuación diferencial estocástica del activo contingente, puede darse una solución al problema de valoración, definiendo previamente:
X n : variable aleatoria con la misma distribución del producto de n variables aleatorias independientes e idénticamente distribuidas, cada una distribuida de la misma forma que la variable aleatoria Y definida en (15), con X0 = 1.
εn: valor esperado de Xn
Por lo que la solución de (25) para el precio de una opción call europea bajo el modelo de saltos de Merton (1976) es la siguiente:
La ecuación (26) no posee una solución cerrada, sin embargo, Merton (1976) señala en su trabajo que existen dos casos especiales en los que (26) puede ser simplificada: el primer caso es la "ruina inmediata", en el que si el evento Poisson ocurre, el precio del subyacente cae hasta 0. El resultado del modelo de Merton en este caso lleva a la fórmula Black-Scholes afectada por una tasa libre de riesgo mayor (r ' = r + λ).
El segundo caso implica que la variable aleatoria Y sigue una distribución lognormal, para lo cual se definen:
δ 2: varianza del logaritmo de Y
En este caso, Xn ~ LN, con,
Ahora, se especifica una nueva expresión para Black-Scholes:
donde:
fn(S,t) valor de la opción estándar del modelo Black-Scholes con varianza v2n y tasa libre de riesgo rn .
Bajo estas condiciones, la ecuación (26) puede definirse como (Merton, 1976):
donde:
Merton (1976) explica que fn (S, t) es el valor de la opción, condicional a conocer el número exacto de n saltos Poisson que ocurrirán en la vida de la opción. El valor de la opción F(S, t) es la suma ponderada de cada uno de estos precios, donde cada peso es igual a la probabilidad de que una variable aleatoria Poisson con parámetro λ, t tome el valor n.
Hemos descrito la metodología de valoración empleada por Merton para una acción que no paga dividendos en la vida del contrato (opción); ya que el propósito de este trabajo es la aplicación de modelos de valoración de opciones sobre divisas, trabajaremos bajo el esquema propuesto por diversos autores (Merton, 1973; Kou, 2007), en el que el componente de tendencia que describe la dinámica del subyacente puede ser expresado de la siguiente forma (bajo la probabilidad P bajo la metodología de valoración riesgo neutral):
Para el caso de acciones que pagan dividendos en la vida del contrato, expresados como δ, como una proporción del precio spot del subyacente, y
Para el caso de divisas, donde rD y rF corresponden a las variables definidas anteriormente. Teniendo en cuenta que la solución inicial de Merton no posee una solución analítica (lo cual es deseable en el marco de este trabajo), se contará con el segundo caso especial, ya que el primer caso podría entenderse como una situación extrema de mercado. En este esquema, la siguiente modificación es necesaria para el problema de valoración de opciones sobre divisas (a partir de allí se utiliza la fórmula (27)):
2.3 Modelo Vanna-Volga de Castagna-Mercurio
El supuesto de volatilidad constante ha llevado a que las opciones con distintos strikes y vencimientos sean valoradas con volatilidades implícitas diferentes, por lo que se reconoce la existencia de una estructura de volatilidad dependiente del strike conocida como smile de volatilidad (Castagna y Mercurio 2006). Por lo anterior, Castagna-Mercurio describen un modelo de mercado para valorar opciones sobre divisas europeas a través de la construcción de la mencionada estructura.
2.3.1 Supuestos del modelo
Castagna-Mercurio trabajan bajo los mismos supuestos del modelo de Black-Scholes (por extensión también aplican los supuestos del modelo de Garman-Kohlhagen):
OΔstraddle, Risk Reversal y Vega-Weighted Butterfly
Las últimas dos condiciones son mencionadas por los autores, y serán necesarias por claridad para el desarrollo del modelo.
2.3.2 Dinámica del subyacente
La dinámica del subyacente es la misma descrita por Garman-Kohlhagen:
donde μ se define como el diferencial de tasas de interés descrito en el modelo de Garman-Kohlhagen.
Castagna y Mercurio desarrollan el modelo desde las tres estructuras más activas del mercado, las cuales fueron mencionadas anteriormente; a partir de estos datos se pueden inferir tres volatilidades básicas, a partir de las cuales se puede construir la estructura de volatilidad. Las cotizaciones de volatilidad se expresan en términos del delta de la opción, para rangos desde 5Δ put hasta el 5Δ call. Se definen:
St : precio spot de la tasa de cambio.
rD: tasa de interés libre de riesgo doméstica.
rF: tasa de interés libre de riesgo del exterior.
T: tiempo al vencimiento.
La volatilidad ATM (at the money) que se cotiza en el mercado cambiario es la del OΔstraddle, estructura en la cual para cualquier T se define el strike para que la opción call y put tengan el mismo Δ con signos diferentes (de esta manera, no se necesita cobertura Δ o delta-hedge). Si se define σATM como la volatilidad ATM para un vencimiento T, y KATM como el strike ATM, se debe cumplir la siguiente condición:
donde:
Φ: función de distribución acumulada normal estándar
Al despejar KATM se obtiene:
La estructura Risk Reversal consiste en la compra de un call y la venta de un put con Δ simétrico. La cotización es la diferencia entre las dos volatilidades implícitas, σ25Δc Y σ25Δp halladas en la metodología Black-Scholes; al definir el precio de cotización en términos de volatilidad se llega a,
Finalmente, la estructura Vega-Weighted Butterfly consiste en la venta de un straddle ATM y la compra de 25Δstrangle. La cantidad del straddle debe ser menor a la del strangle, ya que su Vega (sensibilidad del precio de la opción ante cambios en la volatilidad) es mayor. El precio de cotización del butterfly en términos de volatilidad se define,
Para cualquier T, las volatilidades implícitas σ25Δc Y σ25Δp pueden ser halladas resolviendo un sistema lineal de ecuaciones:
Los K correspondientes a σ25Δc Y σ25Δp, pueden definirse aplicando (29):
donde:
donde:
-Φ_1 = distribución normal inversa.
α > 0, K25Δp < KATM < K25Δc bajo condiciones normales de mercado.
Una vez definidas las expresiones para las tres volatilidades básicas y sus correspondientes strikes, el siguiente paso es construir portafolios Vega-neutrales. Castagna-Mercurio (2006) señalan que se debe derivar un portafolio de cobertura para una opción call europea con tiempo al vencimiento T y strike K, cuyo precio de no arbitraje corresponde a la fórmula de Black-Scholes y Garman-Kohlhagen.
Se pretende entonces encontrar ponderadores en el momento t expresados como χ1 (t; K), χ2(t; K) y χ3(t; K) tales que el portafolio resultante de calls europeas con tiempo al vencimiento T y strikes K1 K2 y K3 respectivamente (los cuales reemplazan a K25Δp, KATM y K25Δc), cubra las variaciones de precio del call con tiempo al vencimiento T y strike K hasta el segundo orden (derivadas parciales respecto al subyacente y volatilidad).
Asumiendo una posición delta hedged, y trabajando bajo el esquema Black-Scholes en el que portafolios de opciones plain vanilla con el mismo T que son Vega neutral también son Gamma neutral (Castagna y Mercurio, 2006), pueden encontrarse los pesos χ1 (t; K), χ2(t; K) y χ3(t; K) bajo la imposición de que el portafolio replicante tiene el mismo Vega, Volga y Vanna que el call con strike K; lo anterior implica:
Se define V (t; K) como el Vega en el momento t de una opción europea con vencimiento T y strike K:
Ahora se calculan las derivadas de segundo orden:
Finalmente, se encuentra la solución al sistema de ecuaciones (38), (39) y (40):
donde:
si K=Kj, entonces χ1(t; K) = 1 para i = j y 0 de otra forma.
2.3.3 Fórmula de valoración
Castagna y Mercurio (2006) definen el precio de una opción call europea a través de una expresión que es consistente con los precios de mercado de las tres opciones básicas:
Los autores sugieren que el precio de un call con strike K, que es consistente con el smile de volatilidad, se obtiene al sumar al precio obtenido de Black-Scholes el costo de implementar la estrategia de cobertura explicada anteriormente, la cual está ajustada a precios de mercado (Castagna y Mercurio, 2006). La expresión obtenida en (50) denota el precio del call europeo en el momento t = 0.
La ecuación (50), que denota el precio del call en función del strike K, sigue las siguientes condiciones de no arbitraje (Castagna y Mercurio, 2006):
3. Aplicación de modelos de valoración de opciones sobre USD-COP
3.1 Caracterización estadística de la serie USD-COP
Para el análisis de la serie se tomaron los precios de cierre históricos del mercado interbancario spot USD-COP; el mercado cambiario goza de alta liquidez a nivel relativo respecto a otros mercados en Colombia, como el de renta variable, e incluso llega a compararse con el mercado de renta fija, con la diferencia de que la liquidez de este último tiende a concentrarse en ciertas referencias y no en todos los nodos de la curva de deuda soberana.
El horizonte temporal de la serie de tiempo seleccionada abarca desde 31/ jul/2009 a 30/sep/2014. Se cuenta con un total de 1348 observaciones obtenidas de Bloomberg de la serie de cierres diarios, a partir de las cuales se calcularon los retornos logarítmicos y se realizaron pruebas de normalidad (figuras 1 y 2).
Con el fin de establecer el cumplimiento de la hipótesis de normalidad que demandan los modelos analizados, se aplicaron pruebas estadísticas como el gráfico Q-Q y el ajuste del histograma a la distribución normal. Para el primer caso comparamos los percentiles de la serie de retornos logarítmicos con los percentiles teóricos de la distribución normal, mientras que en el segundo caso se compara un histograma de los retornos a la curva gaussiana.
Si bien no se presenta un ajuste perfecto para ninguno de los dos casos, se muestra un nivel de ajuste aceptable en la prueba Q-Q, mientras que en el segundo caso se observa claramente que la curva de distribución de los retornos es leptocúrtica. Los test de normalidad más conocidos: Andreson-Darling, Kolgomorov-Smirnov y Jarque-Bera, arrojan como resultado que se rechaza la hipótesis nula de normalidad de la serie (figuras 3 y 4).
Otro de los supuestos más fuertes de los modelos analizados es la estacionariedad, que implica que la media y varianza son constantes a través del tiempo, como lo asume el modelo Black-Scholes. Utilizamos la prueba de Dickey-Fuller aumentada para detectar la presencia de raíces unitarias, con un nivel de significancia de 5 %, rechazando la hipótesis nula (presencia de raíces unitarias) y probando que la serie cumple con la característica de estacionariedad débil.
Se realizaron pruebas de autocorrelación de los retornos logarítmicos. Los gráficos de autocorrelación simple y autocorrelación parcial (figuras 5 y 6) demuestran que los datos presentan perfecta autocorrelación consigo mismos (lag = 0), pero descartan la presencia de fenómenos autorregresivos o de media móvil, lo que confirma la hipótesis de independencia.
3.2 Estimación de los parámetros
Para la estimación de los parámetros de los modelos de Garman-Kohlhagen y Castagna-Mercurio se utiliza el método de máxima verosimilitud siguiendo el trabajo realizado por el profesor John Moreno (2011) dado que, como explica el autor, existen casos particulares donde el método puede ser aplicado de forma directa a parir de conocer la función de densidad de probabilidad del proceso del subyacente en la ecuación.
De manera general, los modelos de Garman-Kolhagen y de Black-Scholes son representados por la EDE:
Donde β y σ son los parámetros constantes desconocidos, y representan los componentes de tendencia y difusión respectivamente.
De acuerdo con lo enunciado por Moreno (2011), se obtienen los siguientes estimadores para el caso de la media y varianza:
donde:
n: número de datos de la variable.
yi: dato u observación puntual de la serie de retornos logarítmicos diarios. A partir de las expresiones anteriores se obtienen los estimadores para la EDE:
Ahora que se cuenta con las expresiones para los parámetros de tendencia y difusión, se aplican los mismos a la serie de datos USD-COP. A partir de este punto seguiremos el trabajo realizado por Brigo, Damiano, Neugebauer y Triki (2008), con el fin de calibrar la serie de tiempo al modelo GBM. Se sugiere como primera medida encontrar los estimadores iniciales para la serie de tiempo analizada, por lo que tenemos:
El código utilizado para esta estimación se describe en detalle en Brigo et al. (2008). El segundo paso es simular la distribución de los retornos y la volatilidad (varianza), por lo que se obtienen los siguientes resultados (figuras 7 y 8):
Luego de hallar los estimadores iniciales, y a través del método de máxima verosimilitud, llegamos a la estimación final de los parámetros (tabla 2):
Finalmente, una vez encontrados los parámetros de la distribución normal, se realiza una simulación base 100 sobre la distribución del precio del activo (USD-COP) y se comprueba que sigue una distribución lognormal (ya que en los pasos anteriores se ajustó una distribución normal a los retornos logarítmicos, se puede asumir que el subyacente cumple este supuesto). En este punto hemos probado, bajo ciertas condiciones, que el comportamiento del subyacente del derivado (tasa de cambio USD-COP) puede ser modelado a través del GBM generalizado. Anteriormente hemos probado el supuesto de estacionariedad débil a través de la prueba Dickey-Fueller, a la vez que comprobamos el principio de independencia de la serie a través de las pruebas de correlación. Cabe resaltar, sin embargo, que la serie original presentó problemas de ajuste de los retornos a la distribución normal, como se evidenció en las pruebas Anderson-Darling, Kolgomorov-Smirnov y Jarque-Bera. Por esta razón, al momento de seleccionar el modelo del comportamiento del subyacente se siguió la metodología propuesta por Brigo et al. (2008) (figura 9).
Para el caso del modelo de Merton, se hace necesario encontrar estimadores para tres parámetros: λ, el cual describe el número de saltos por unidad de tiempo; δ, que representa la desviación estándar del proceso lognormal de los saltos, y m, el valor esperado (media) del proceso lognormal. El autor opta por los modelos de Garman-Kohlhagen y Castagna-Mercurio para la aplicación, ya que se cuenta con límites de información para calibrar el modelo de Merton.
4. Aplicación de los modelos de valoración de opciones
En este apartado aplicaremos los modelos analizados y evaluaremos su viabilidad como metodología propuesta para la valoración de opciones europeas sobre tasa de cambio en el mercado colombiano.
4.1 Supuestos y consideraciones
Precios opciones europeas (implícitos). Como aproximación a los precios históricos del derivado, tomaremos como base los indicadores de volatilidad implícita ATM a 1 y 2 meses obtenidos de Bloomberg; a partir de esta información se infieren precios de opciones europeas call y put implícitos, como herramienta de control. Las consideraciones sobre el precio spot y las tasas de interés son aplicadas como se describió anteriormente. Esto implica simular las condiciones de un ambiente de mercado real.
4.2 Resultados del ejercicio
4.2.1 Strike ATM
Se tomaron los datos de volatilidad implícita de mercado a 1 mes y strike ATM, con el fin de encontrar los precios implícitos de las opciones europeas libres de arbitraje. A través de la aplicación de los modelos de Castagna-Mercurio (Vanna-Volga) y Garman-Kohlhagen se obtuvieron los siguientes resultados (tabla 3):
4.2.2 Strike Put-Call Parity
Para este escenario se trabajó con los datos de volatilidad implícita de mercado a dos meses y strike que cumplen la paridad put-call, y se obtuvo lo presentado en la tabla 4.
4.2.3 Strike ITM y OTM, Smile de volatilidad
En el mercado de opciones sobre divisas, el precio de los derivados con diferentes strikes y tiempo al vencimiento se cotiza con diferentes volatilidades implícitas, este factor es conocido comúnmente como el smile de volatilidad. Otros autores se refieren a este efecto como la tendencia a denominar la volatilidad como una función del strike en un horizonte de tiempo determinado.
La existencia de este efecto permite que el mercado asigne a través del precio diversos niveles de riesgo a diferentes escenarios en el futuro, lo cual es una característica deseable. Teniendo en cuenta la revisión de los modelos analizados, cabe recordar que uno de los supuestos del modelo de Garman-Kohlhagen es el de volatilidad constante (al igual que Black-Scholes).
En otras palabras, el modelo de Garman-Kohlhagen supone que el nivel de volatilidad se mantiene para todos los niveles de strike y tiempo al vencimiento; por su parte, el modelo Vanna-Volga permite derivar una expresión analítica para la construcción del smile de volatilidad a partir del precio de la opción europea, la cual es consistente con el principio de no arbitraje. Esta última característica brinda una poderosa ventaja al modelo teniendo en cuenta que, si bien a través del modelo de Garman-Kohlhagen se puede construir el smile de volatilidad (y también la superficie por definición), se tiene que abandonar uno de los supuestos básicos.
Castagna-Mercurio (2006) demuestran dos expresiones que permiten la construcción del smile de volatilidad en su artículo. En el avance de esta investigación se desarrollaron códigos para las dos definiciones, sin embargo, los autores señalan que la aproximación que se describe a continuación es más robusta:
Las expresiones para K1, K2, K3, d1 y d2, fueron definidas en la sección 2. Como ejercicio de validación del modelo y de los códigos desarrollados en la investigación, se procede a replicar el ejemplo propuesto en el artículo de Castagna-Mercurio (2006), bajo las siguientes condiciones: divisa= EUR-USD, spot = 1.205, σATM = 9,05%, σRR = -0,50%, σVWB = -0,13%, rD = -0,03794, rF =-0,02139, T= 94/365, obteniendo los siguientes resultados (tabla 5):
Como segunda validación se construye el smile de volatilidad del artículo, como se muestra a continuación, y a través de los inputs propuestos se llega a los niveles de volatilidad implícita ATM del documento (9,05 %), lo cual da una tercera validación del resultado (figura 10).
Aplicando el modelo se construye un smile de volatilidad hipotético para el caso del mercado de opciones colombiano, con los siguientes parámetros a corte 30/enero/2015: divisa = USD-COP, spot = 2439, σATM = 15,23%, σRR = 2,05%, σVWB = 0,41%, rD = 4,40, rF = 0,25, T = 2/12, para llegar a (figura 11):
La construcción del smile de volatilidad permite encontrar los niveles implícitos para opciones ITM, por lo que a través de la expresión encontramos (tabla 6):
Ahora, simulamos la aplicación del modelo Vanna-Volga con niveles de strike OTM (tabla 7):
5. Conclusiones
Se han analizado en detalle dos modelos de valoración de opciones sobre divisas, con el fin de aplicarse al mercado colombiano. El modelo Vanna-Volga de Castagna-Mercurio presenta sólidos niveles de ajuste para la valoración de opciones call y put europeas sobre USD-COP, consistentes con el modelo clásico de Black-Scholes y su extensión de Garman-Kohlhagen cuando la opción se encuentra ATM (para este tipo de opción ambos modelos presentan niveles de ajuste satisfactorios). El modelo Vanna-Volga permite encontrar niveles de volatilidad consistentes cuando la opción se encuentra ITM y OTM.
Si bien el modelo de Garman-Kohlhagen también puede llegar a niveles de ajuste que son sólidos y comparables con el de Castagna-Mercurio para opciones ITM y OTM, es necesario abandonar uno de los supuestos básicos como es la volatilidad constante. Abandonar este supuesto permite la construcción del smile de volatilidad.
La expresión analítica para el smile de volatilidad en el modelo Vanna-Volga le brinda capacidad superior de ajuste respecto a otros modelos con solución analítica, sumado a su facilidad de implementación.
El movimiento browniano geométrico generalizado puede encontrarse como un modelo de ajuste aceptable que cumple con las condiciones mínimas necesarias para ser considerado el proceso estocástico que describe el comportamiento del subyacente (tasa de cambio USD-COP). Se abre la discusión sobre otros modelos que podrían representar un mejor ajuste.
La revisión en detalle de la solución analítica de los modelos analizados se convierte en uno de los aportes de este trabajo. Uno de los principales obstáculos para la implementación de otros modelos reside en la calibración de los parámetros, problema que recibe especial atención en la academia y ha motivado importantes avances.
Este trabajo presenta una introducción para futuras investigaciones sobre el tema de valoración de opciones, en el cual el campo de acción se amplía a medida que se abandonan los supuestos del modelo básico de Black-Scholes, o se trata el problema de valoración de derivados más complejos.
Referencias
Black, F. (1976). The pricing of commodity contracts. Journal of Financial Economics 3(1-2), 167-79.
Black, F. y Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy 81(3) 637-54.
Brigo, D., Dalessandro, A., Neugebauer, M. y Triki, F. (2008). A Stochastic Processes Toolkit for Risk Management. 1-43. Recuperado de http://www.damianobrigo.it/toolboxweb.pdf.
Castagna, A. y Mercurio, F. (2006). Consistent pricing of fx options. Recuperado de http://www.fabiomercurio.it/consistentfxsmile.pdf.
Clavijo, S. (2001). El régimen de flotación cambiaria en Colombia. Recuperado de http://www.banrep.gov.co/sites/default/files/publicaciones/archivos/flotacion1.pdf.
Garman, M. B. y Kohlhagen, S. W. (1983). Foreign currency option values. Journal of International Money and Finance 2(3), 231-37.
Hull, J. (2012). Options, Futures and Other Derivatives (8 ed.). Toronto: Pearson.
Kou, S. G. (2007). Jump-Diffusion models for asset pricing in financial engineering. Handbooks in Operations Research and Management Science 15(C), 73-116.
Merton, R. C. (1973). Theory of rational option pricing. Bell Journal of Economics 4(1), 141-83. Recuperado de http://www.jstor.org/stable/3003143.
Merton, R. C. (1976). Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics 3(1-2), 125-44.
Moreno, J. (2011). Estimación de parámetros en ecuaciones diferenciales estocásticas aplicadas a finanzas. ODEON 6, 131-44.
Samuelson, P. (1965). Rational Theory of Warrant Pricing. Industrial Management Review 6(2), 13-31.
Samuelson, P. y Merton, R. C. (1969). A complete model of warrant pricing that maximizes utility. Industrial Management Review 10(2), 17-46.
Villar, L. (1999). Política cambiaria en un proceso de ajuste ordenado. Recuperado de http://www.banrep.gov.co/docum/Lectura_finanzas/pdf/politcambi.pdf.