10.18601/17941113.n22.02

Patrones de comportamiento de clientes con tarjetas de crédito de consumo con deterioro de calificación por riesgo utilizando K-means

Costumer behavior with credit cards with deterioration of the risk rating using K-means

Diego Barragán Garnica*

* Magíster en Finanzas. Financial Management Specialist at Banco Davivienda, Bogotá (Colombia). [diegobarragan041@gmail.com]; [ORCID ID: 0000-0003-3308-5592]

Para citar este artículo:
Barragán Garnica, D. (2022). Patrones de comportamiento de clientes con tarjetas de crédito de consumo con deterioro de calificación por riesgo utilizando K-Means. Odeon, 22, 7-37. DOI: https://doi.org/10.18601/17941113.n22.02

Artículo recibido: 16 de mayo de 2022. Aceptado: 25 de mayo de 2022.

Resumen

En este documento se presenta el análisis del comportamiento de los clientes con tarjetas de crédito de una institución financiera colombiana con base en su calificación de riesgo de crédito, a través de la aplicación del modelo de machine learning no supervisado denominado K-means. Se obtienen clústeres de clientes que permiten identificar sus patrones de comportamiento.

Palabras clave: modelo K-means; machine learning; tarjetas de crédito; calificación de riesgo de crédito.
Clasificación JEL: C63, C69, C88, C89.

Abstract

This document presents the analysis of the behavior of cardholders of a Colombian financial institution based on their credit risk rating through the application of the unsupervised machine learning model called K-means. Clusters of clients are obtained that allow identifying their behavior.

Key words: K-means; machine learning; credit cards; credit score.
JEL classification: C63, C69, C88, C89.

Introducción

La gestión de riesgo de crédito, a través de los sistemas de administración de riesgos, contribuye a la estabilidad del sistema financiero; sin embargo, como en todos los mercados, esto no contempla su eliminación, pero sí permite a las instituciones de crédito detectar, mitigar y contar con la información histórica de la evolución de sus indicadores1. Por otro lado, los sistemas de administración de riesgo deben considerar aspectos tanto cuantitativos como cualitativos, siendo esta gestión un proceso integral que permite una adecuada medición. A lo largo del tiempo, para las instituciones y los establecimientos de crédito, el sistema de administración y gestión del riesgo de crédito se ha convertido en uno de los pilares estratégicos de continuo monitoreo, que preserva la estabilidad del sistema financiero y que, bajo una buena gestión, contribuye a mayores utilidades reportadas en los estados de resultados, en donde es de vital importancia tener un conocimiento integral de los clientes y su riesgo de crédito asociado.

En el segmento de personas la banca tradicional, así como enfoca sus estrategias por productos, en la gran mayoría también enfoca su gestión de riesgos por productos, de acuerdo con sus distintas líneas de negocio. Es de gran importancia interpretar y analizar comportamientos del cliente para identificar patrones de comportamiento diferencial o similar entre ellos, y así entender el comportamiento del portafolio de crédito. De esta manera, las entidades y los establecimientos de crédito pueden evaluar mejor las fortalezas, debilidades, riesgos y oportunidades que influyen en sus portafolios y, de forma prospectiva, pueden anticipar cambios en las tasas de mora del cliente, reflejado en sus diferentes portafolios de cartera como un menor gasto de provisión. En este punto, dada la cantidad de información que manejan estas entidades financieras, las herramientas y metodologías de Data Mining, Machine Learning y Big Data permiten a estos negocios analizar grandes volúmenes de datos, y descubrir nuevos conocimientos y aplicaciones para una toma de decisiones más asertiva.

A continuación, se presentarán algunas cifras mencionadas en el Reporte de Estabilidad Financiera del primer y segundo semestre de 2020 publicado por el Banco de la Republica. En uno de sus componentes hace referencia a que la cartera destinada a los hogares2 corresponde a 260,7 billones de pesos colombianos con un crecimiento real anual del 10,7 % en el primer semestre y del 3,9 % en el segundo semestre, mostrando una desaceleración dada la coyuntura; para el primer semestre, el crecimiento fue jalonado por la cartera de consumo con un incremento real anual del 12,4 %, y con la misma relación la cartea de consumo presentó una fuerte desaceleración creciendo el 3,2 % para el II semestre. Es importante mencionar el crecimiento alcista sostenido de la cartera de tarjetas de crédito con una participación aproximada del 20 % en la cartera de consumo en el primer semestre.

En términos de riesgo de crédito, la cartera de consumo en el reporte del primer semestre muestra crecimientos en la cartera vencida y la riesgosa ubicándose en 7,7 y 4,9 % respectivamente, con corte a junio de 2020. Sin embargo, la calidad de cartera, al menos en el corto plazo, podría tener un deterioro dado un impacto negativo en la capacidad de pago de los hogares. Estos mismos indicadores para el segundo semestre, con corte a septiembre de 2020, se ubican en 8,7 y 4,9 % respectivamente, esperando mayores deterioros a finales de 2020 dada la salida de algunos alivios otorgados a los deudores para los pagos de sus obligaciones.

Por otro lado, según las cifras de la Superintendencia Financiera de Colombia (Banco de la República, 2020), para el año 2019 el sistema bancario generó utilidades por 10,9 billones de pesos, con gasto por deterioro de la cartera de 22,9 billones de pesos, representando un 25 % del total de los gastos para este periodo; sin embargo, esta participación ha aumentado un 4 % en el total de gastos del sistema bancario con cifras a junio 2020, y con cifras a diciembre de 2020 la participación es del 28 % con un aumento de 300 pbs comparado con junio del mismo año.

Como se mencionó, la volumetría de datos que tienen las entidades y los establecimientos de crédito propicia el uso de herramientas y modelos de análisis de datos, y, en general, la industria bancaria y financiera debe desarrollar estrategias centradas en el cliente, siempre con una gestión de riesgos activa, en este caso una gestión de riesgo de crédito, identificando las distintas variables que permitan tener un adecuado seguimiento y mitigación.

El objetivo de este documento es identificar los patrones de uso de clientes con tarjetas de crédito de consumo antes del incumplimiento de pago o cambio de calificación de crédito por mora. En este artículo, un modelo eficiente y con un alto componente de interpretación, que forma parte de la familia de modelos no supervisado K-means, permitirá caracterizar el comportamiento transaccional de los clientes con tarjetas de crédito con calificaciones de riesgo de crédito diferentes de "A" al cierre del año 2019, a través de la conformación de clúster, y se implementará con datos reales de una muestra de clientes de una entidad financiera. Las variables más relevantes para el desarrollo de este documento son la facturación de compras y avances mensual en cada una de las calificaciones de riesgo por mora y comercios en donde estos clientes facturan, y luego se describirán y se compararán los resultados arrojados por cada uno de estos grupos.

Para ello, el documento se divide en cuatro secciones. La primera sección presenta las generalidades de la cuantificación y el registro del gasto de provisión de las entidades de crédito. La segunda se enfoca en la descripción teórica del modelo K-means y algunas aplicaciones en la industria de tarjetas de crédito. La tercera sección muestra la aplicación del modelo con datos de clientes durante al año 2019. Finalmente, se presentan las conclusiones del documento.

1. Marco de gestión del riesgo crediticio-Sistema de Administración del Riesgo Crediticio

En la Circular Básica Contable y Financiera (Circular Externa 100 de 1995) se establece la reglamentación necesaria y que debe ser adoptada y aplicada para la gestión de riesgo de crédito a los establecimientos de crédito con operación en Colombia. De manera general se dará un contexto de la constitución de provisiones como un rubro muy importante dentro del estado de resultados de estas entidades; pues bien, esta constitución de provisiones se define para las modalidades de cartera comercial, vivienda, consumo y microcrédito, que para este caso se centrará en la modalidad de consumo dado el enfoque del desarrollo del documento.

En términos generales, el Sistema de Administración del Riesgo Crediticio (SARC) debe estimar o cuantificar las pérdidas esperadas de cada modalidad de crédito y resulta de la aplicación de la siguiente formula:

Pérdida Esperada = [Probabilidad de incumplimiento] x [Exposición del activo] x [Pérdida esperada de valor del activo dado el incumplimiento]

Las especificidades para la cartera de consumo se encuentran el anexo 5 del capítulo 2, "Gestión del riesgo de crédito", de la Circular 100 de 1995, que en el marco del Modelo de Referencia para la Cartera de Consumo (MRCO) indica la metodología de calificación de los deudores, bajo la metodología de fase acumulativa o desacumulativa:

  1. Calcular el puntaje para el cliente, así:

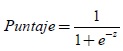
    2. Donde, Z varía de acuerdo con el segmento al cual pertenece el deudor. A continuación, se especifica el valor de Z para el portafolio de tarjetas de crédito donde las entidades deben aplicar la siguiente fórmula:

    Z = - 1.824 + MMB * 1.214 + MMC * 1.313 + MMD * 3.469 + AMB * 2.350 + AMC * 3.525 - PR * 0.6 + CAR * 0.748 + CAM * 2.470 + CRB * 0.277

    Variable prepago: esta variable se construye comparando la cuota esperada (intereses esperados + capital esperado) por parte del deudor frente a la cuota pagada (intereses pagados + capital pagado), y PR ("Prepago"): toma valor 1 si el cliente, al momento de la calificación, no tiene mora mayor a 30 días y si la cuota recibida es significativamente mayor que la esperada.

  2. De acuerdo con el puntaje anterior, ubicar al cliente en la siguiente matriz (tabla 1):

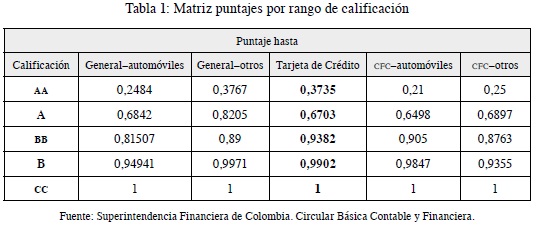
  3. Identificar la probabilidad de incumplimiento: corresponde a la probabilidad de que en un lapso de 12 meses los deudores de un determinado segmento y calificación de cartera de consumo incurran en incumplimiento y que, dada la fase en cual se encuentra, aplicará la matriz A o B (tablas 2 y 3).

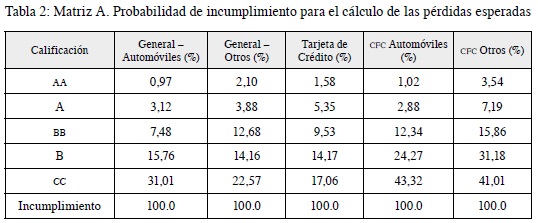
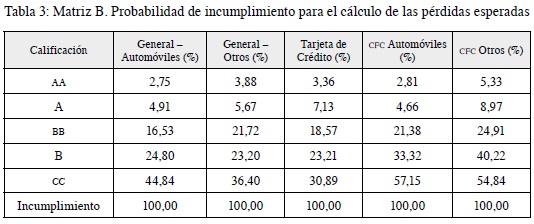
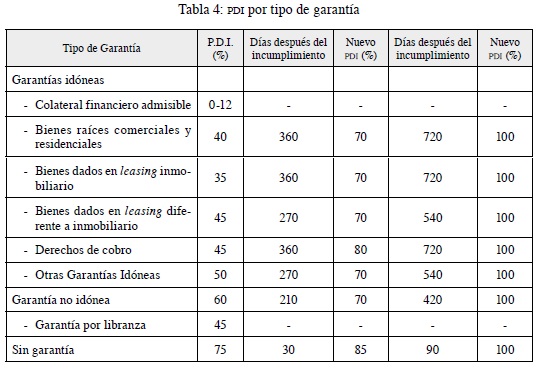
  4. La pérdida dado el incumplimiento (PDI): se entiende por incumplimiento el evento en el cual una operación de crédito de consumo se encuentra en mora mayor a 90 días, o que siendo reestructurada incurra en mora mayor o igual a 60 días. La PDI por tipo de garantía será la siguiente (tabla 4):

    5. La exposición del activo es su valor expuesto, entendido como el saldo de la obligación al momento del cálculo de la pérdida esperada. Aquellas entidades que dispongan de información histórica pertinente podrán calcular la exposición de los derechos contingentes a través de métodos de reconocido valor técnico3.

2. Modelo no supervisado K-means

Los métodos de aprendizaje automático más utilizados en la industria se clasifican, en general, en los métodos de aprendizaje no supervisado, supervisado, semisupervisado y con refuerzo. De acuerdo con Zhiqiang, Zhihuan Song, Steven X. Ding y Biao Huang, los métodos de aprendizaje no supervisados tienen el objetivo principal de explorar los datos y encontrar alguna estructura oculta entre ellos, y para ello las técnicas más comunes son: análisis de componentes principales, modelos de mezcla gaussiana, Hierarchical clustering o agrupamiento jerárquico, regresiones lineales, regresión logística, análisis discriminante, árboles de decisión, máquina de vector soporte, vecinos más cercanos, redes neuronales.

Dadas las múltiples alternativas de métodos de aprendizaje automático y en relación con el abordaje literario en el estado del arte, se propone usar el modelo de K- means clustering dada su amplia aplicación en la industria y sus ventajas en términos de interpretación y explicación, el cual se describe a continuación.

• K-means clustering

Este método de aprendizaje hace parte de los métodos de solución de agrupamiento, los cuales son más complejos que los métodos de clasificación. ¿Y por qué es importante la agrupación? Pues bien, la agrupación se ha utilizado para obtener información sobre los datos, generar hipótesis, detectar anomalías e identificar características sobresalientes, también se usa para identificar el grado de similitud entre formas u organismos (relación filogenética) o se usa como método para organizar los datos y resumirlos a través de prototipos de clúster.

Los algoritmos de agrupamiento se pueden dividir en dos grupos, los jerárquicos y los particionales. Aquellos algoritmos que encuentran de modo aglomerativo y recursivamente grupos anidados (comenzando con cada punto de datos en su propio grupo y fusionando el par de grupos más similares sucesivamente para formar una jerarquía de grupos) o en modo divisivo de arriba hacia abajo (comenzando con todos los puntos de datos en un grupo y dividiendo recursivamente cada grupo en grupos más pequeños) se denominan jerárquicos, y los particionales son aquellos que encuentran todos los grupos simultáneamente como una partición de los datos y no imponen una estructura jerárquica.

Entonces, bajo la anterior contextualización, el K-means es un método de agrupamiento particional cuyo objetivo es dividir las muestras de datos de n observaciones en k agrupaciones diferentes, en las que cada muestra de datos pertenece al agrupamiento con la media más cercana, es decir, que cada observación esté en el grupo más cercano con la distancia más corta a su media de grupo correspondiente o centroide. El algoritmo parte de la fijación de k centroides aleatoriamente, y mediante un proceso iterativo se asigna a cada punto al clúster con el centroide más próximo, procediendo a actualizar el valor de los centroides; este proceso termina cuando se alcanza determinado punto de convergencia. Matemáticamente lo que hace el algoritmo es: Supongamos que tenemos n puntos de observación x1, x2, ... , xn en un espacio vectorial d-dimensional, el objetivo es dividir estas observaciones en k grupos (S1, S2,..., Sk) con medios centroides (µ1, µ2,..., µk), de modo que la suma de grupos de cuadrados, también llamada suma de cuadrados dentro del clúster, se puede minimizar, es decir,

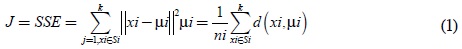
Ecuación 1. Minimización errores al cuadrado

Ecuación 2. Cálculo centroide.

Donde: 1 < k ≤ n ; k < n.

El objetivo de K-means es minimizar la suma de los cuadrados sobre todos los grupos de K, sin embargo, este algoritmo solo puede converger a un minimo local, y a medida que el número de grupos k aumenta el error cuadrático disminuye (con J = 0 cuando K = n). Una forma de superar los mínimos locales es ejecutar el algoritmo K-means, para un K dado, con múltiples particiones iniciales diferentes y elegir la partición con el error al cuadrado más pequeño. De acuerdo con lo anterior, el algoritmo K-means necesita tres parametros: el número de clústeres K, inicialización de clúster y métrica de distancia, donde k es el parámetro más crítico de estimar. Comúnmente, K-means se ejecuta independientemente para diferentes valores de K y se selecciona la partición que parece más significativa para el experto en el dominio. Sin embargo, existen multiples formas (Jain, 2010) para hallar el valor de k óptimo, entre otras:

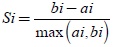
Ecuación 3. Minimización errores al cuadrado

Donde:

ai: promedio de las distancias entre la observación i y el resto de observaciones que pertenecen al mismo clúster.

bi: menor de las distancias promedio entre i y el resto de clústeres, es decir, la distancia al clúster más próximo.

Sin embargo, muchas de las inquietudes están direccionadas a conocer el mejor algortimo para agrupación de datos, cuando ya se tengan las estimaciones adecuadas. Jain (2010), dentro de su investigación especifica que existe la similitud entre los algoritmos de agrupamiento que se mide como la similitud promedio entre las particiones obtenidas en los conjuntos de datos, por lo cual los algoritmos se pueden agrupar de acuerdo con su similitud medida con el Índice de Rand Ajustado. De gran importancia son las conclusiones que encontraron Fisher y van Ness (1971), quienes analizaron detalladamente los algoritmos para generar una orientacion, definiendo criterios de admisibiidad como convexo, proporción de conglomerados, omisión de clúster y monotonía, demostrando que no se pueden contruir algoritmos que satisfagan todos los criterios. A ellos se ratifica Kleinberg (2002) quien definió como criterios invarianza de escala, riqueza y consistencia llegando a una conclusión similar, de ahí el título de su artículo "Un teorema de imposibilidad para la agrupación".

La determinación del mejor algoritmo de agrupamiento la impone la estructura en los datos, ya sea explícita o implícitamente, que se ve reflajada en la buena dinámica entre el modelo y los datos. Dado que la estructura de los datos no se conoce a priori, se debe probar e intentar con varios enfoques competitivos la determinación de un algoritmo apropiado para la tarea de agrupamiento en cuestión.

Por otro lado, una vez se halla el número óptimo de clústeres, existe la técnica llamada validación cruzada de los métodos, que se basa en comparar los cuatro métodos de K-means para elegir el mejor y así obtener los mejores resultados. Estos métodos son: Lloyd, Forgy, MacQueen y Hartigan-Wong, y la forma de seleccionar el más óptimo entre estos es el método que maximice la distancia intraclúster, que es la suma de las distancias entre los centroides de los clústeres.

Según el documento "The k-means clustering technique: General considerations and implementation in Mathematica" (Morissette y Chartier, 2013), los algoritmos de Lloyd y de Forgy se denotan con el centroide más próximo y cada centroide se asigna al final de cada ciclo del proceso de asignar cada individuo al clúster (de los K prefijados) con el centroide más próximo. En el caso del algoritmo MacQueen, para cada dato se calcula la distancia más cercana con sus vecinos y si el centroide del subespacio al que pertenece es el más cercano, no se realiza ningún cambio, pero si otro centroide es el más cercano se reasigna al otro centroide, y estos se recalculan como la media de los casos correspondientes; como se describe, estos tres algotimos se basan en el cálculo de los centroides, sin embargo, este último calcula cada centroide a partir de los miembros del clúster tras cada asignación y no al final de cada ciclo como en Forgy y el algoritmo de Lloyd.

Por otro lado, el algoritmo Hartigan & Wong, a diferencia de los anteriores que usan el cálculo de la menor distancia en comparación con el centroide, lo que hace es encontrar el óptimo local mediante la reducción de la suma de los errores intraclúster de los cuadrados y, de esta manera, se asigna cada dato al mejor clúster correspondiente.

Una vez se selecciona el K y el algoritmo o método óptimo para obtener los clústeres de los datos y proceder con el análisis, se evalúa el modelo por medio de medidas de estabilidad y validación de la composición de los difentes clústeres.

Algunas de las medidas con las que se evalúan las caracteristicas de los clústeres son las medidas de estabilidad como medidas de validación interna que generan eliminación de datos y recálculos de forma iterativa de los clústeres, entre ellas se encuentran:

Average proportion of non-overlap (APN): mide la proporción media de observaciones que no se asignan al mismo clúster cuando se elimina una columna del set de datos en comparación con cuando se incluyen todas.

Average distance (AD): mide la media de las distancias promedio intraclúster empleando todos los datos y eliminando una columna a la vez.

Average distance between means (ADM): mide la media de las distancias entre centroides empleando todos los datos y eliminando una columna a la vez.

Figure of merit (FOM): mide la media de la varianza intraclúster de la columna eliminada, empleando la estructura del clustering calcula con las columnas no eliminadas.

Los valores de APN, ADM y FOM pueden ir desde 0 a 1, los valores pequeños son un indicativo de alta estabilidad. En el caso de AD ocurre lo mismo, pero sus valores pueden ir de 0 hasta infinito.

De gran importancia también son el coeficiente de silueta que se mencionó anteriormente y el índice de DUNN que consiste en verificar que los conjuntos de clúster estén bien compactos internamente, pero muy bien separados entre clúster, por lo cual la maximización de este índice muestra un mejor clúster; el cálculo del índice DUNN se realiza a través de la siguiente expresión:

DI = min(min{dist(Xi, Xj)})/(max {diam(Xk)}), 1 ≤ k ≤ nc

Ecuación 4. Minimización errores al cuadrado

Donde:

nc: número de clúster.

Dist (Xi, Xj): distancia entre dos clústeres.

Diam (Xk): máxima distancia entre los elementos de un clúster.

3. Aplicación del modelo: tarjetahabientes Banco Davivienda

3.1 Comprensión del negocio

El negocio de tarjetas de crédito se basa en la concepción de ser el método de pago seguro y recurrente del cliente, cuyo crecimiento depende de la cantidad de lientes adquiridos, en adquisición, retención y fidelización, a través de la colocación de una línea de crédito revolvente por parte de las entidades de crédito autorizadas por la autoridad financiera, en el caso colombiano, la Superintendencia Financiera. Por medio de esta línea de crédito, se realizan compras, avances o compras de cartera de otras entidades financieras, y es un negocio en donde el comportamiento de pago de cada cliente refleja las tasas de morosidad tanto en el portafolio de tarjetas de crédito como en los demás productos del activo, lo que impacta de manera negativa los resultados o las utilidades de la línea de negocio y de la entidad de crédito.

3.2 Comprensión de los datos

Los datos que se utilizarán son de los clientes actuales del Banco Davivienda que se encuentran en la bodega de datos de esta entidad. Pueden ser de tipo cualitativo o cuantitativo, y se usarán los siguientes (tabla 5):

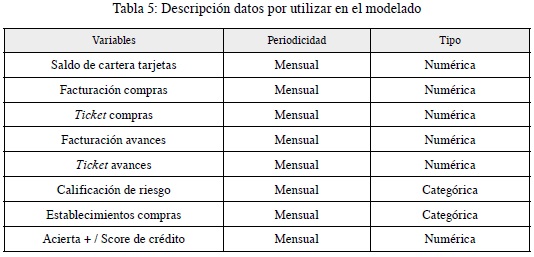
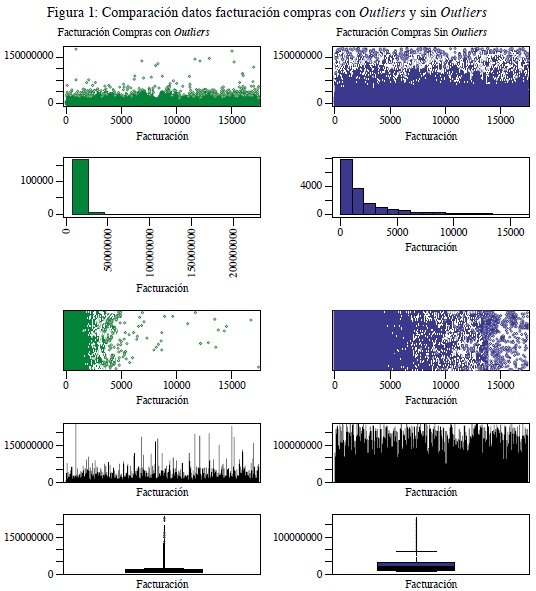
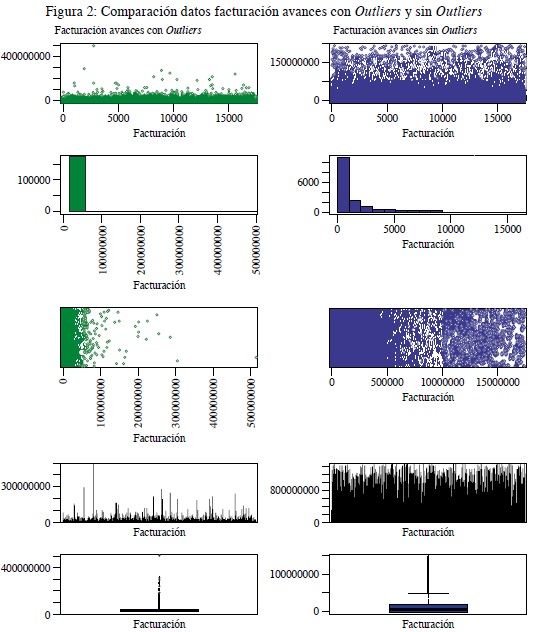
Esta información se trabajará con una periodicidad mensual del año 2019. Se realizarán las transformaciones pertinentes, completitud de la información, análisis de datos atípicos y pruebas estadísticas para evitar conclusiones erradas luego de la comprensión y preparación de los datos.

La base de datos por analizar es una muestra aleatoria del total de clientes, con su comportamiento mensual en facturación, que permite tener una evolución y comportamiento de facturación en cada una de las calificaciones. Al momento de correr el modelo de K-means con los respectivos índices de estabilidad, con una cantidad datos superior a la muestra aleatoria, la memoria no era la suficiente, por lo cual se decidió trabajar con una muestra de 17.449 clientes, quienes a corte de diciembre de 2019 tuvieron una calificación diferente de A.

3.3 Modelado

Dada la revisión de bibliografía, en la mayoría de los trabajos de investigación, para la agrupación de los datos y el comportamiento de estos se utiliza el modelo de K-means; así se obtiene cierto número de clústeres que permitan entender y analizar su comportamiento.

Algunas de estas aplicaciones las podemos ver en Edelman (1992), en donde, para un banco comercial de Escocia se realizó un análisis de la morosidad de las cuentas observadas en cada mes durante un periodo de 2 años y se llevó a cabo una agrupación utilizando el método de agrupamiento de k-medoides con distancia euclidiana; el objetivo principal del análisis se basó en identificar grupos de clientes y una combinación de clientes y productos.

Adams, Hand y Till (2001), en su artículo "Minería para clases y patrones en datos de comportamiento", analizan un conjunto de datos de comportamiento de un gran banco del Reino Unido en relación con el estado de las cuentas corrientes durante un periodo de doce meses. Se usan los enfoques de agrupamiento convencionales, por ejemplo, para definir categorías amplias de comportamiento, mientras que la búsqueda de patrones se puede usar para encontrar pequeños grupos de cuentas que exhiben un comportamiento distintivo.

En el trabajo "Credit card customer segmentation and target marketing based on data mining" (Li et al., 2010), los clientes de tarjetas de crédito de un banco comercial chino se agrupan en cuatro clasificaciones por K-means: cliente de alta calidad, cliente potencial de alta calidad, cliente común y cliente desfavorable.

Soukal y Hedvicaková (2011), con el trabajo "Procedia computer retail core banking services e-banking client cluster identification", se enfocan en el mercado minorista de servicios bancarios centrales, en su gran mayoría a consumidores en el mercado de la Unión Europea, en donde se analizan los datos a través de conglomerados basado en el algoritmo k-means. Al realizar el análisis de conglomerados se obtuvieron conclusiones como: hay clientes que comparten la preferencia de internet como el canal de comunicación, sin embargo, su uso mensual de retiros es 2-3 veces mayor en comparación con el cliente promedio; otros clientes, a diferencia del cliente promedio (39,3 % de participación), tienen una menor actividad en un 50 % en retiros, aunque la preferencia de internet es la misma.

Por otro lado, en el artículo "Applying data mining to insurance customer churn management" (Soeini y Rodpysh, 2012), en la modelación de los datos los autores utilizaron para el agrupamiento el método K-means y usaron la minimización de los errores cuadráticos para seleccionar el número de clúster. El número de clúster para el desarrollo de la investigación es cuatro. Posterior a esto, se aplicó un árbol de decisión para conocer los clientes de posible abandono de la compañía.

Martins y Cardoso (2012), en su investigación "Cross-validation of segments of credit card holders" evalúan la segmentación de los tarjetahabientes a través de la validación cruzada. El enfoque propuesto es la segmentación aplicada en una institución financiera portuguesa, específicamente a clientes premium que tienen al menos una tarjeta dorada.

Algunas de las variables que se incluyen dentro del modelo son información general del cliente, información sobre su relación e interacción con la organización, información sobre saldos, rentabilidad, crédito rotativo, crédito dirigido a crédito personal, pagos, impagos, uso de tarjetas, compras, adelantos en efectivo y algunas categorías de gastos.

Posteriormente, se identifica que las variables discriminantes entre los grupos son: estado del cliente con respecto a su actividad transaccional, cantidad de compras en los últimos 12 meses, valor gastado en compras en los últimos 12 meses, proporción de meses con uso de tarjeta en los últimos 24 meses, saldo promedio de crédito en los últimos 12 meses. Con los anteriores diferenciadores, la segmentación que resulta del método de validación cruzada es: clientes de alto uso de tarjetas de crédito, clientes con un alto uso de crédito rotativo, clientes de uso moderado de tarjeta de crédito, clientes orientados al uso de débito, y clientes con muy poco uso de tarjeta de crédito.

A su vez, en el artículo "Credit card behavior, financial styles, and heuristics" (Shefrin y Nicols, 2014), el cual realiza varias contribuciones en el ámbito de manejo de tarjetas de crédito, estudia los datos que provienen de dos encuestas realizadas en mayo y junio de 2009. Ambas encuestas se centran en obtener características y patrones de comportamiento de los titulares de tarjetas de crédito que están asociados con la especificidad de los objetivos financieros.

Pues bien, para la segmentación de los clientes encuestados, los autores utilizaron el método de K-means y obtuvieron como resultados cuatro clústeres, así: Pagadores mínimos de bajo control, Pagadores mínimos de alto control, Saldo total y múltiples titulares de tarjetas, Saldo total y únicos titulares de tarjetas.

Desde otro enfoque, como lo es el análisis de riesgo, en el artículo "Identification of credit risk based on cluster analysis of account behaviours" (Bakoben et al., 2019) se estudia un conjunto de datos de la tarjeta de crédito que incluye comportamientos mensuales para 494 cuentas activas de una institución financiera anónima en el Reino Unido, por un periodo máximo de 37 meses desde junio de 2008 hasta junio de 2011. El objetivo con estos datos es asignar clientes en grupos basados en sus comportamientos mensuales y así discriminar entre clientes de alto y bajo riesgo.

3.4 Caso de aplicación: clientes del Banco Davivienda

Como parte metodológica, una vez entendido el comportamiento del negocio y los datos por utilizar, en términos generales, se modelarán los clústeres de clientes a través del modelo K-means aplicado a los datos de los clientes del Banco Davivienda.

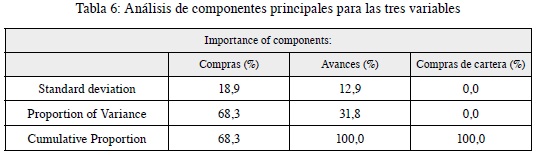
Como se mencionó, un cliente tiene tres formas de usar el cupo de su tarjeta de crédito: facturación en compras, facturación en avances y facturación en compras de cartera; de esta manera, para reducir el manejo de las variables y explicar en gran medida el comportamiento de todos los clientes, se aplica un análisis de componentes principales (ACP). Para aplicar este acp se reemplazaron los outliers y se normalizó la serie de datos para obtener resultados consistentes. Como se observa en la en la tabla 6, la facturación en avances y la facturación en compras son las variables que explican el 100 % de la varianza, por lo cual el análisis de clúster se realiza con estos dos tipos de facturación de los clientes.

Al reducir la dimensionalidad, excluyendo la variable compras de cartera, se normalizan los datos de la facturación en compras y avances con el método de reescalado, que permite estandarizar la medida de los datos y obtener beneficios computacionales al momento de procesar los datos. Este método utiliza la siguiente expresión para normalizar las variables:

(x - min(x))/(max(x) - min(x))

En donde x = registro o dato de la base de datos.

Ecuación 5. Reescalado de los datos para normalizarlos

Con la estandarización de las variables y eliminando los efectos de los outliers, dado que el modelo K-means en muy sensible a este tipo de comportamiento en las variables, se procedió a aplicar el método Elbow que permite identificar la cantidad óptima de centroides (k) por utilizar, ya que no necesariamente se conoce con anterioridad, y con ayuda de este método se busca seleccionar la cantidad ideal de grupos a partir de la optimización, a través de la minimización de la suma interna de cuadrados (figura 3).

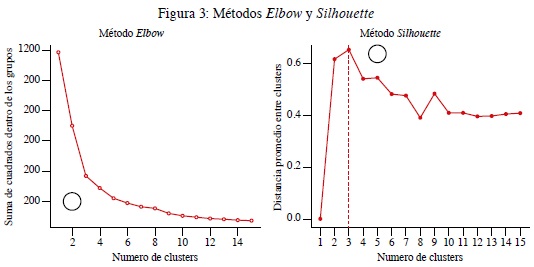
Como complemento al método Elbow, para encontrar el número de clúster se aplicó a los datos el método average silhouette, en donde se maximiza la media de los coeficientes silhouette o coeficientes silueta.

De acuerdo con la optimización, dado el método de elbow y el de average silhouette, se seleccionaron tres clústeres, ya que es aquel punto en donde disminuye la suma de los errores al cuadrado de manera significativa y aquel punto en donde se maximiza la media del silhouette coeficiente de todas las observaciones como se evidencia en las figuras anteriores, lo que permite identificar claramente tres grupos de clientes para los respectivos análisis. Una vez seleccionados los tres clústeres, para optimizar el algoritmo K-means existen cuatro formas de este algoritmo: Lloyd, Forgy, MacQueen y Hartigan-Wong y la manera de conocer el mejor algoritmo dentro de estos es utilizar la "distancia intraclúster", que es la suma de las distancias entre los centroides, por tanto, el mejor desempeño es aquel algoritmo con mayor distancia intraclúster ya que es la mejor separación entre cada clúster. Una vez aplicados estos algoritmos, como muestra la tabla 7, el algoritmo de K-means Hartigan-Wong es el ganador dado que la distancia intraclúster es la más alta. Sin embargo, las diferencias con los demás algoritmos son muy pequeñas, pero al momento de hablar de optimización es el mejor algoritmo.

La figura 4 muestra los tres clústeres de clientes que se obtienen del modelo K-means con una explicación del 95 % de la varianza de los datos, en donde el clúster 1 está compuesto por 79 % de clientes, el clúster 2 por de 11 % clientes y el clúster 3 por 10 % de clientes.

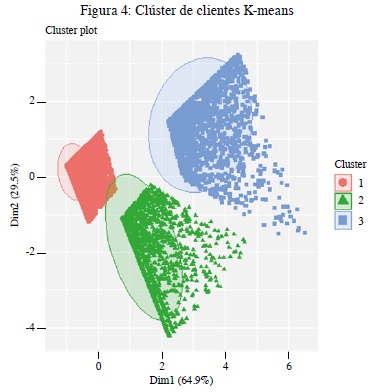
Dado que se debe validar la estructura y composición de los clústeres de clientes, las tablas 8 y 9 permiten ratificar la validación interna y externa de los mismos. En la tabla 8 se comparan las medidas de estabilidad a través de los tres métodos más comunes y utilizados de clustering, con la finalidad de comparar el modelo de desarrollo de este documento K-means con modelos como el PAM y Hierarchical.

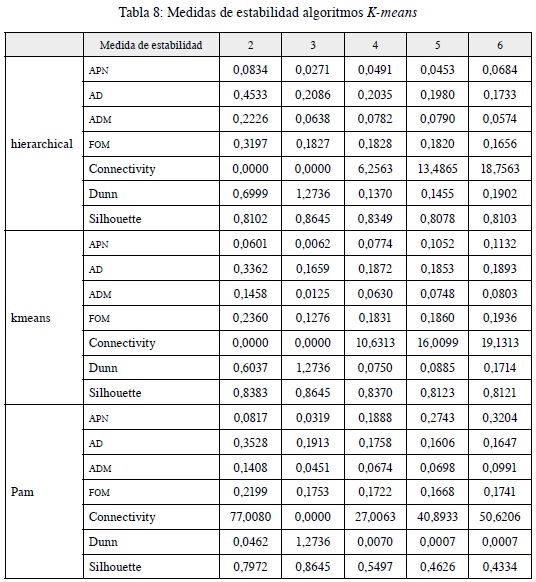
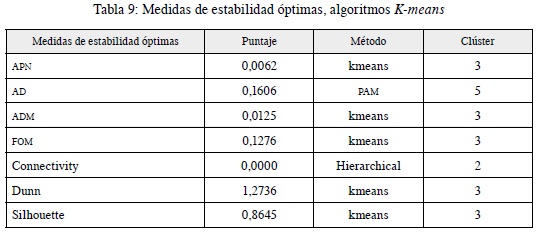
Recordemos que valores pequeños de APN, ADM y FOM son un buen indicativo de estabilidad y en el caso del Índice DUNN, conectividad y Silhouette a mayor número, mejor indicativo de estabilidad. De tal manera, como se puede observar para el número de tres clústeres las medidas ya mencionas o maximizan o minimizan dependiendo de la mejor interpretación en cuanto a estabilidad se refiere, para los tres métodos: K-means, PAM y Hierarchical en una comparación entre dos y seis clústeres.

Una vez analizado desde otra metodología el número óptimo de clústeres (3), se identifican los valores de las medidas de estabilidad y el mejor método de acuerdo con la estructura y la información contenida en los datos insumo para el análisis. Estos resultados se evidencian en la tabla 9, en donde K-means es el método con los mejores resultados.

Ahora bien, comenzando a describir el comportamiento y las características de los clústeres, dado que se está trabajando con clientes que registraron un deterioro de la calificación de crédito, y dado que en el sistema financiero la variable acierta es de gran relevancia al momento de evaluación de crédito, se describen los clústeres y la totalidad de los clientes respecto a esta variable cuantitativa con un rango hasta 1000 puntos, que a mayor puntaje indica mejor comportamiento y pago de las obligaciones de crédito del sistema financiero (se debe aclarar que esta variable no se tomó en cuenta al momento de la generación de los clústeres).

Según Data crédito, el acierta es un

… modelo de score de crédito desarrollado por Experian Colombia S.A. consistente en un esquema estadístico que se basa en el comportamiento y hábito de pago histórico de los colombianos con el objeto de permitirle a las entidades de crédito conocer la probabilidad de cumplir con una obligación en los próximos 90 días en los próximos 12 meses, de sus clientes actuales o potenciales.

A continuación, en la figura 5 se observa que para el total de los clientes el 60 % de estos tiene un score inferior al promedio del acierta total.

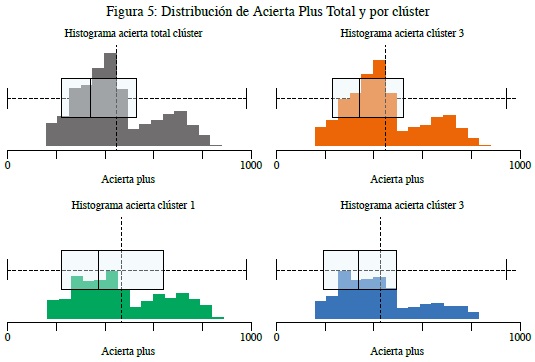
Al analizar los diferentes clústeres con la variable acierta y por calificación de riesgo, encontramos:

El clúster 1, como el más poblado con un 79 % de la muestra de clientes seleccionada, revela que el 75 % de los clientes tiene un acierta 0,2 veces mayor al promedio del acierta del total de clientes.

El clúster 2, con un 11 % de la muestra de clientes seleccionada revela que 75 % clientes tiene un acierta 0,4 veces mayor al promedio del acierta del total de los clientes.

El clúster 3, con un 10 % de la muestra de clientes seleccionada indica que el 75 % clientes tiene un acierta 0,1 veces mayor al promedio del acierta del total de clientes.

Al incluir esta variable, que no se tuvo en cuenta al momento de agrupar los clústeres, es muy interesante lo que se extrae como información de estos, pues el 75 % de clientes tiene aciertas muy bajos y, por otro lado, se observa que es una característica compartida en cada uno de los clústeres.

Entrando un poco más en detalle, en la tabla 10 se muestra la cantidad de clientes en cada clúster, diferenciados por calificaciones y su respectivo comportamiento en cuanto a facturación de compras y avances.

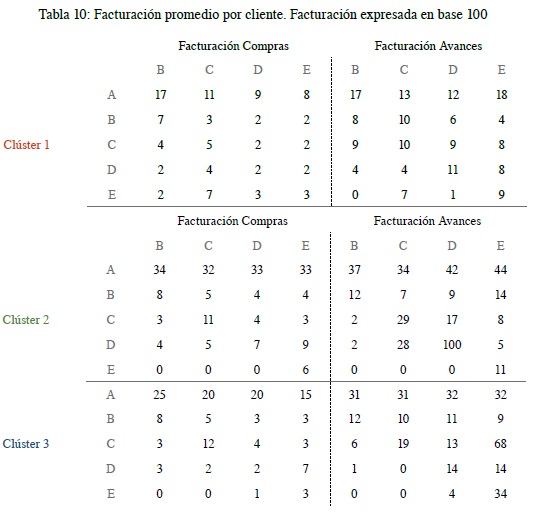
En la tabla 10, de manera horizontal se observan los clientes que a diciembre de 2019 tuvieron calificaciones diferentes de A, y verticalmente las calificaciones en las que estuvieron estos mismos clientes a lo largo del año 2019, con su facturación mensual, calculada únicamente sobre los meses en los que hubo uso de la tarjeta de crédito. Para entenderlo mejor se usará el primer dato de 17 cuya interpretación es: dentro del clúster 1 los clientes que a diciembre de 2019 tuvieron una calificación B, pero durante los meses de 2019 estuvieron con calificaciones A, facturaron 17 mensualmente.

Como se evidencia en la tabla 10, el clúster 2 es aquel con mayor facturación por cliente tanto en compras como en avances, sin embargo, no es el más representativo en cantidad de clientes. Este clúster, en comparación con el clúster 1, factura en compras entre dos y tres veces más y, comparado con el clúster 3, entre una y dos veces más. En cuanto a facturación en avances, en comparación con el clúster 1 factura en entre dos y cuatro veces más, y comparado con el clúster 3 una vez más.

Por otro lado, el clúster 1 es el más representativo en número de clientes, se describe con una facturación ponderada por cliente en compras de aproximadamente 10 y facturación en avances de aproximadamente 14. El clúster 2 tiene una facturación ponderada por cliente en compras de aproximadamente 22 y facturación en avances de aproximadamente 35, y el clúster 3 con el 10 % factura 16 y 29 respectivamente. Con este comportamiento, se evidencia que la facturación de avances en esta población es más alta que la facturación de compras, dependiendo del clúster, entre una y dos veces de mayor facturación, recordemos que estas cifras de facturación están expresadas en base 100.

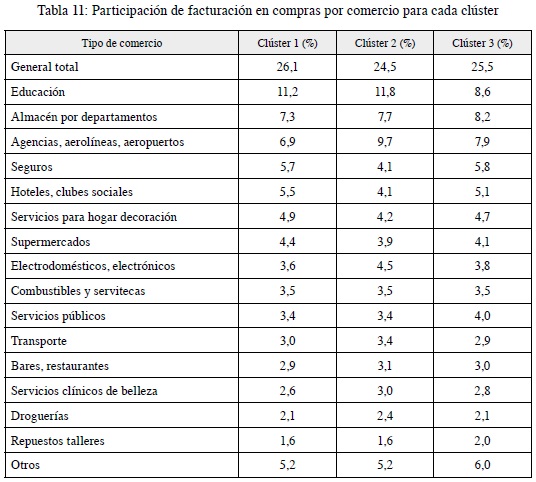
Al analizar el comportamiento de la facturación en compras, de acuerdo con el comercio o categoría de comercio, se encuentra que para los tres clústeres existe un comportamiento similar en términos de la proporción destinada de gastos de los clientes en estos comercios. Sin embargo, las compras destinadas a educación para el clúster 2 representan un 11,8 %, mientras que para el clúster 3 representan el 8,6 %. También se observan diferentes comportamientos por compras en electrodomésticos y electrónicos, supermercados y agencias, aerolíneas y aeropuertos, hoteles y clubes sociales (tabla 11).

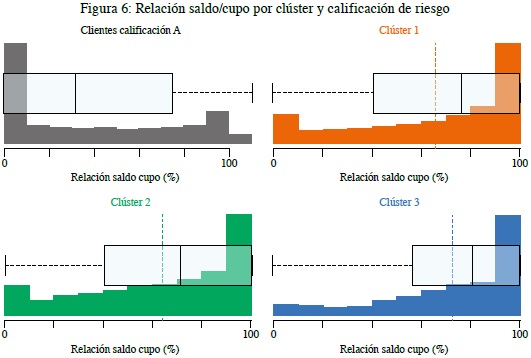
Ahora, como complemento del análisis se aborda el comportamiento de estos clientes desde la relación deuda/cupo, que tiene cada uno de ellos al corte de diciembre de 2019, entendiendo la deuda como el valor adeudado por cliente a la entidad financiera producto del uso de la tarjeta de crédito y, por otro lado, el cupo como el valor total del crédito aprobado por el Banco.

Como se observa en la figura 6, en primer lugar, los clientes con calificación A, descritos como clientes con un excelente comportamiento de pago de sus obligaciones, a corte de diciembre de 2019 representan, en un 75 %, clientes que tienen una relación saldo/cupo menor o igual al 80 % y un 5,7 % con una relación del 100 %. Sin embargo, al analizar este mismo comportamiento por cada uno de los clústeres se evidencia:

4. Conclusiones

El modelo no supervisado K-means es uno de los modelos más utilizados y de gran interpretabilidad al momento de segmentar o clasificar clientes, en este caso, de la industria bancaria, que permite identificar en cada uno de los grupos de clientes patrones de comportamiento comunes y diferenciales dentro de los mismos. Aplicado a la base de datos de los clientes con tarjeta de crédito arrojó como resultados tres clústeres de clientes que muestran estabilidad y muy buena interpretación al momento del análisis interno de cada uno.

Analizar el comportamiento de crédito de los clientes por medio de estas herramientas de analítica de datos se traduce automáticamente en una de las mejores prácticas de gestión y minimización de riesgos que tienen un gran impacto en los Estados de resultados de las entidades financieras, mejorando sus utilidades.

De acuerdo con los resultados del modelo K-means el 75 % de los clientes de cada uno de los clústeres tiene un puntaje de acierta bajo y, por ende, estos clientes muestran calificaciones de riesgo bajas.

La facturación en compras para los tres presenta un comportamiento similar en términos de la proporción destinada de gastos de los clientes en estos comercios, sin embargo, para estas categorías de electrodomésticos y electrónicos, supermercados y agencias, aerolíneas y aeropuertos, hoteles y clubes sociales se observan pequeños diferenciales relativos de gasto en los clústeres.

Se evidencia que la facturación de avances unitaria de los clientes de los tres clústeres es más alta que la facturación de compras, dependiendo del clúster, entre una y dos veces de mayor facturación comparada con la facturación en compras.

Entre el 30 y el 38 % de los clientes de los clústeres tienen una relación deuda/cupo del 100 %, es decir, no tienen cupo disponible para uso y, por ende, en este producto su endeudamiento es del 100 %.

Notas

1 Según lo establecido en el capítulo II de la Circular Básica Contable y Financiera (Circular Externa 100 de 1995) de la Superintendencia Financiera de Colombia, capítulo que introduce las Reglas relativas a la gestión del riesgo crediticio.
2 Por cartera destinada a los hogares se entiende la suma de las carteras de consumo y de vivienda con titularizaciones otorgadas por establecimientos de crédito, Fondo Nacional del Ahorro (FNA), cooperativas de ahorro y crédito, y fondos de empleados.
3 El valor expuesto del activo, definición capítulo II, Reglas relativas a la gestión del riesgo crediticio, Circular 100 1995 SFC.

Referencias

Accenture (2019). 2019 Global Financial Services Consumer Study. Accenture.

Adams, N. M., Hand, D. J. y Till, R. J. (2001). Mining for classes and patterns in behavioural data. Journal of the Operational Research Society, 52 (9), 1017-1024.

Banco de la República (2020). Informe especial riesgo de mercado. Banrep.

Bakoben, M., Bellotti, T. y Adams, N. (2019). Identification of credit risk based on cluster analysis of account behaviours. Journal of the Operational Research Society, 0(0), 1-9. https://doi.org/10.1080/01605682.2019.1582586

Edelman, D. B. (1992). An application of cluster analysis in credit control. IMA Journal of Management Mathematics, 4(1), 81-87. https://doi.org/10.1093/imaman/41.81

Eduardo, C., López, B., Alfredo, J., García, J., Antonio, J. y López, V. (2019). Bancaria por métodos estadísticos y redes neuronales artificiales usando r. Resumen, 40(132), 43-63.

Fisher, L. y Ness, J. W. V. (1971). Admissible clustering procedures. Biometrika, 58 (1), 91-104.

Ge, Z., Member, S., Song, Z. y Ding, S. X. (2017). Data Mining and Analytics in the Process Industry: The Role of Machine Learning, IEEE access, 5.

Grosan, C. (2011). Evolution of Modern Computational. En Intelligent Systems, Springer. 1-11.

Hsieh, N. (2004). An integrated data mining and behavioral scoring model for analyzing bank customers. Expert Systems with Applications, 27(4), 623-633. https://doi.org/10.1016/j.eswa.2004.06.007

Hearst, M. A., Dumais, S. T., Osuna, E., Platt, J., y Scholkopf, B. (1998). Support vector machines. IEEE Intelligent Systems and their applications, 13(4), 18-28.

Jain, A. K. (2010). Data clustering: 50 years beyond K-means q. Pattern Recognition Letters, 31(8), 651-666. https://doi.org/10.1016/j.patrec.2009.09.011

Kleinberg, J. (2002). An impossibility theorem for clustering. Advances in neural information processing systems, 15.

Li, W., Wu, X., Sun, Y. y Zhang, Q. (2010). Credit card customer segmentation and target marketing based on data mining. Proceedings-2010 International Conference on Computational Intelligence and Security, CIS 2010, 73-76. https://doi.org/10.1109/CIS.2010.23

Buchanan, B. G. (2005). A (Very) Brief History of Artificial Intelligence. AAAI Publications, 53-60.

Martins, M. C. y Cardoso, M. (2012). Cross-validation of segments of credit card holders. Journal of Retailing and Consumer Services, 19(6), 629-636. https://doi.org/10.1016/j.jretconser.2012.08.004

Minskyt, M. (s. d.). Steps Toward Artificial Intelligence. Proceedings of the IRE.

Morissette, L. y Chartier, S. (2013). The k-means clustering technique: General considerations and implementation in Mathematica. Tutorials in Quantitative Methods for Psychology, 9(1), 15-24. https://doi.org/10.20982/tqmp.09.1.p015

Paõ, U., Paõ, U., Vasco, Â., Modron, J. I., Paõ, U. y Paõ, U. (1998). Clients' characteristics and marketing of products: Some evidence from a financial institution. https://doi.org/10.1108/02652320310488420

Pelleg, D. y Moore, A. W. (2000). X-means: Extending k-means with efficient estimation of the number of clusters. Icml, 1, 727-734.

Shefrin, H. y Nicols, C. M. (2014). Credit card behavior, financial styles, and heuristics. Journal of Business Research, 67(8), 1679-1687. https://doi.org/10.1016/j.jbusres.2014.02.014

Scholkopf, B., Smola, A. y Muller, K. (1998). Non-linear component analysis as a kernel eigenvalue problem. Neural Computation, 10(5), 1299-1319. https://doi.org/10.1162/089976698300017467

Soeini, R. A. y Rodpysh, K. V. (2012). Applying Data Mining to Insurance Customer Churn Management, 30, 82-92.

Soukal, I. y Hedvicaková, M. (2011). Procedia computer retail core banking services e-banking client cluster identification. Procedia Computer Science, 3, 1205-1210. https://doi.org/10.1016/j.procs.2010.12.195

Timón, C. E. (2017). Análisis predictivo: técnicas y modelos utilizados y aplicaciones del mismo-Herramientas Open Source que permiten su uso (trabajo de de grado).

Wallace, C. S. y Boulton, D. M. (1968). An information measure for classification. The Computer Journal, 11 (2), 185-194.

Wallace, C. S. y Freeman, P. R. (1987). Estimation and inference by compact coding. Journal of the Royal Statistical Society: Series B (Methodological), 49 (3), 240-252.